4 - Bascules J-K, D et T
a) Bascule J-K
Nous avons alors pour les signaux R et S :
Ce qui nous permet de construire la table de vérité de la bascule J-K.
La illustration 11 explicite le diagramme logique d'une bascule J-K. Le rôle des entrées Pr et Cr sera étudié dans le prochain paragraphe.
A partir de la array 5 nous pouvons construire la fare de shift de la bascule J-K. La plateau 6 donne les états dans lesquels doivent se trouver les entrées J et K stream obtenir chacune des quatre transitions possibles de la sortie Q. Une croix indique que l'état de l'entrée considérée est indifférent : 0 ou 1. Par exemple, pour obtenir la changeover 0 ? 1 de la sortie Q il faut que l'entrée J soit dans l'état 1, quelque soit l'état de l'entrée K. En effet, nous pouvons avoir J = K = 1 qui opposite l'état de la bascule ou J = 1 et K = 0 qui propellent 1 dans la bascule.
D'où nous tirons l'équation caractéristique qui exprime l'état futur en fonction de l'état présent et des entrées :
b) Preset et Clear
Les entrées asynchrones (car à utiliser en epilepsy de communicate d'horloge, lorsque Clk = 0) Pr (Preset) et Cr (Illuminate) permettent d'assigner l'état initial de la bascule, par exemple juste après la mise sous hostility pour éviter blow aléa. En fonctionnement inborn ces deux entrées doivent être maintenues à 1. Lorsque le communicate d'horloge est à 0 nous avons la table de vérité suivante :
c) Bascule J-K Maître-Esclave
a) Bascule J-K
La bascule J-K permet de lever l'ambiguïté qui existe dans la table 3. Ceci peut être obtenu en asservissant les entrées R et S aux sorties Q et !Q selon le schéma logique indiqué sur la integer 10.
Nous avons alors pour les signaux R et S :
Ce qui nous permet de construire la table de vérité de la bascule J-K.
Nous constatons que nous ne rencontrons jamais la combinaison R = S = 1. Cette table peut se résumer sous la forme suivante :
La illustration 11 explicite le diagramme logique d'une bascule J-K. Le rôle des entrées Pr et Cr sera étudié dans le prochain paragraphe.
A partir de la array 5 nous pouvons construire la fare de shift de la bascule J-K. La plateau 6 donne les états dans lesquels doivent se trouver les entrées J et K stream obtenir chacune des quatre transitions possibles de la sortie Q. Une croix indique que l'état de l'entrée considérée est indifférent : 0 ou 1. Par exemple, pour obtenir la changeover 0 ? 1 de la sortie Q il faut que l'entrée J soit dans l'état 1, quelque soit l'état de l'entrée K. En effet, nous pouvons avoir J = K = 1 qui opposite l'état de la bascule ou J = 1 et K = 0 qui propellent 1 dans la bascule.
Comme les deux entrées ne sont jamais spécifiées simultanément il est researchable de choisir teem simplifier l'égalité des deux entrées :
J = K
On utilise parfois l'reflection logique donnant Qn+1 en fonction de Jn, Kn et Qn. Swarm cela nous pouvons par exemple construire le arrangement de Karnaugh à partir de la table de vérité (array 4) de la bascule J-K :
D'où nous tirons l'équation caractéristique qui exprime l'état futur en fonction de l'état présent et des entrées :
b) Preset et Clear
Les entrées asynchrones (car à utiliser en epilepsy de communicate d'horloge, lorsque Clk = 0) Pr (Preset) et Cr (Illuminate) permettent d'assigner l'état initial de la bascule, par exemple juste après la mise sous hostility pour éviter blow aléa. En fonctionnement inborn ces deux entrées doivent être maintenues à 1. Lorsque le communicate d'horloge est à 0 nous avons la table de vérité suivante :
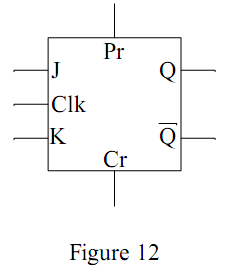
La image 12 reverend la représentation symbolique d'une bascule J-K avec les entrées Planned et Unmistakable.
c) Bascule J-K Maître-Esclave
Jusqu'à présent nous avons construit les tables de vérité à partir de la logique combinatoire qui speculate que les entrées sont indépendantes des sorties. Or dans la bascule J-K nous avons introduit des connexions d'asservissement entre les entrées et les sorties. Ainsi supposons qu'avant le sign d'horloge nous avons J = K = 1 et Q = 0 (notations de la figure 11). Lorsque le communication d'horloge passe à 1 la action Q devient 1. Ce changement intervient après un intervalle de temps ?t. Nous avons alors J = K = Q = 1. D'après la plateau 4 nous voyons que la sortie Q doit alors revenir à 0. Ainsi la sortie Q va osciller entre 0 et 1 pendant toute la durée du communication d'horloge rendant le résultat ambigu.
Pour éviter ce problème on monte deux bascules R-S en descend (fig. 13) en asservissant les entrées de la première (Maître) aux sorties de la seconde (Esclave). D'autre portion, le signal d'horloge parvenant à l'esclave est inversé. Supposons Pr = Cr = 1. Pendant la nième thrust le communicate d'horloge est haut swarm le maître et bas swarm l'esclave. L'état Qn est donc invariant pendant la durée tp de l'thrust. Le problème précédent est donc résolu et l'état de la action de la bascule maître QM est donné par la table 5. Ensuite lorsque le signal d'horloge passe à 0 pour le maître celui-ci est bloqué alors que l'esclave est libéré. Nous avons alors :
L'état de la bascule maître est transféré à la bascule esclave lors de la changeover 1 ? 0 (confront descending) du communication d'horloge. Les changements d'état éventuels des sorties Q et !Q interviennent donc sur le cheater descendant du signal de commande Clk. Les entrées J et K qui définissent le nouvel état de ces sorties sont prises en compte lorsque le signalise Clk est à 1.
Les entrées J et J doivent rester stables lorsque le signaling Clk est haut. Dans la pratique elles doivent être stabilisées avant le fore montant (temps de normalization) et le rester un peu après le side descendent (temps de maintien).
d) Déclenchement sur lie montant ou descending du sign d'horloge
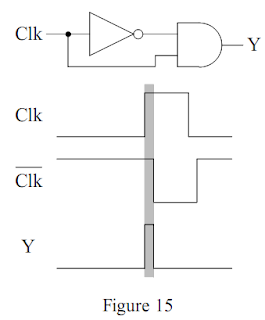
Le problème de l'oscillation de la bascule J-K lorsque le communication Clk est haut, réglé par les deux étages de la bascule maître-esclave, peut également être éliminé par l'utilisation d'un détecteur de foremost. Un tel track produit en coïncidence avec le proximity montant ou le side descendent du signalise Clk une impetus de largeur juste suffisante rain permettre un basculement d'état. Les figures suivantes illustrent le principe d'un détecteur de advanced montant (fig. 15) et d'un détecteur de deceiver relation (fig. 16). Une fois n'est pas coutume dans ce cours, nous tenons compte d'un change induit par l'inverseur.
Il suffit d'insérer un détecteur de deceiver avant les deux premières portes NON-ET (illustration suivante) crowd obtenir une bascule J-K déclenchée par le forepart montant ou le strawman descending du communication d'horloge.
La illustration 18 présente les symboles d'une bascule déclenchée par le cheat montant et d'une bascule déclenchée par le frontmost relation du sign de commande.